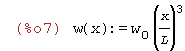
1 Metoda Ritz'a wersja próbna do dalszego doskonalenia
| (%i8) | kill(all)$ |
1.1 Założenia
Metoda Ritz w duzym uproszeczniu polegana aproksymacji rozwiazania równania różniczkowego
PDE z pomocą tkz. rpzwioazań póbnych majacych postać np. wielomianu n tego stopnia
Kroki rozwiązania metodą Ritz'a
krok 1. Zakładamy funkcję "próbną" wiażącą wielkości istotne dla analizowanego problemu
Rozwiazanie próbne powinno spełniać warunki brzegowe danego problemu.
Również warunki fizyczne problemu powinny być spełnine
przykładowo funkcja przemieszczenia w zagadnieniach z wytrzymałości materiałów
może być napisana w postaci
u(x)=C1+C2x+C3x^2 ....
gdzie C1 C2 C3 są poszukiwanymi stałymi
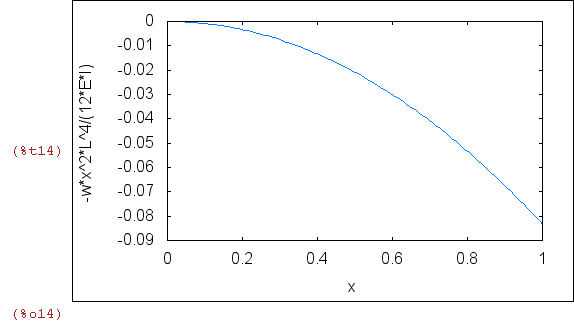
krok 2. Rózniczkowanie i całkowanie wyrażenia ujmującego całkowitą energie potencjalną
| (%i1) | TPE_='integrate(f(u(x)),x); |
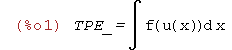
krok 3. Poszukiwanie minimum TPE ze wzgledu na wartości C[i] wytępujące w rozwiązaniu próbnym
| (%i2) | 'diff(TPE_,C[i])=0; |
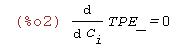
krok 4 rozwiązanie uzyskanych w poprzednim kroku układu równań ze względu na C[i]
Wyznaczenie ostatecznej postaci funkcji u(x) porówanie jej z dostępnym rozwiązaniem analitycznym
1.2 Przykład 1 Nierozciągliwa lina
| (%i3) | kill(all); |
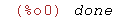
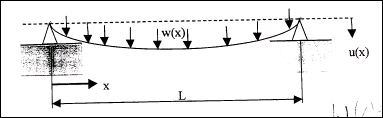
Rozważmy giętki kabel o długości L umocowany w dwóch punktach i obciążony
siłą o intensywności w(x). Określić funkcję u(x) ugięcia kabla.
Obciażenie kabla w(x)=W*x jest liniowe i wynosi zero w punktach podparcia
Figure 1: E:\praca\Maxima_w_przykladach\MetodaRitza_Galerkina\Ritz\Ritz_lina.jpg

Całkowita energia potencjalna układu
| (%i1) | TPE=('integrate((1/2)*T*'diff(u(x),x)^2-w(x)*u(x),x)); |
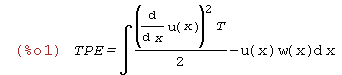
Obciażenie kabla w(x)=W*x jest liniowe i wynosi zero w punktach podparcia
| (%i2) | w(x):=W*x; |
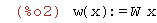
Krok 1
Zakładamy rozwiązanie "próbne' w postaci wielomianu
| (%i3) | u(x):=C[1]*phi[1](x)+C[2]*phi[2](x); |
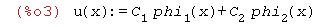
gdzie funkcje phi[1](x) i phi[2](x) są dobrane tak aby spełniały warunki
brzegowe to jest:
dla x=0 u(0)=0
x=L u(l)=0
| (%i4) |
phi[1](x):=(x/L)*(1-x/L); phi[2](x):=((x/L)^2)*(1-x/L); |
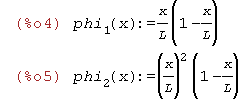
funkcja u(x) przymuje postać
| (%i6) | u(x); |
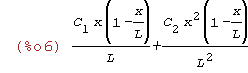
Obliczamy pochodną up(x) funkcji u(x) po x
| (%i7) | upp(x):=diff(u(x),x); |
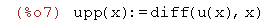
Krok 2
Dla giętkiego kabla obciażonego siłami pionowymi o inetnsywności w(x) całkowita energia potencjalna
TPE jest obliczana z:
| (%i8) | TPE:integrate((1/2)*T*diff(u(x),x)^2-w(x)*u(x),x,0,L); |
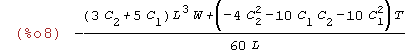
Krok 3
Itotą metody Ritz'a jest obliczanie warotści C1 i C2 dajacych minimum funkcji TPE_
| (%i9) | 'diff(TPE_,C[i])=0; |
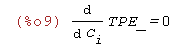
Obliczamy pochode TPE po stałych C1 i C2 i przyrównujemy je do zera
| (%i10) | eq1:diff(TPE,C[1]); eq2:diff(TPE,C[2]); |
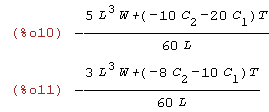
Krok 4
Poszukujemy wartości C1 i C2 po rozwiązaniu układu równań eq1=0 ieq2=0
| (%i12) | roz:solve([eq1=0,eq2=0],[C[1],C[2]]); |
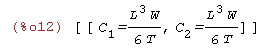
Krok 5
Budujemy ostateczną formę wyrażenia opisujacego linię ugiecia liny u(x)
z uwagi, że otrzymane rozwiązanie składa się z dwu elementów zagnieżdżonych dwukrotnie
stosujemy podwójen indeksowane.
| (%i13) | C[1]:rhs(roz[1][1]); C[2]:rhs(roz[1][2]); |
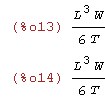
| (%i15) | u(x); |
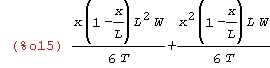
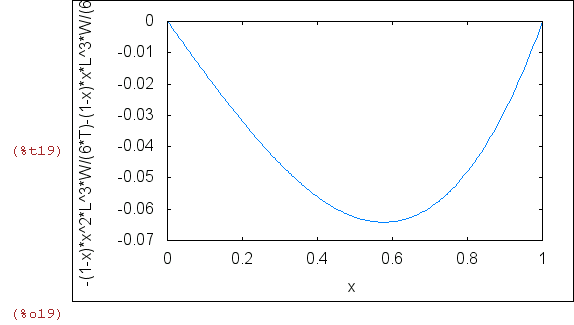
kreślenie lini ugięcia liny
dla L=1 W=1, T=1
| (%i16) | L:1; W:1; T:1; |

| (%i19) | wxplot2d(-u(x),[x,0,L]); |
1.3 Przykład 2 Belka wspornikowa
| (%i20) | kill(all); |
Analizę wpływu stopnia wielomianu aproksymujacego na jakość rozwiązania w metodzie Ritz'a
prześledzimy na przykładzie belki wspornikowej
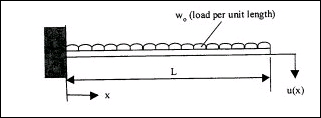
Rozważmy belkę wspornikową jednostronie utwierdzoną, obciążoną obciążeniem ciągłym
o intensywności w(x)=w. Określić funkcję u(x) ugięcia belki.
Figure 2: E:\praca\Maxima_w_przykladach\MetodaRitza_Galerkina\Ritz\Ritz_wspornik.jpg
Całkowita energia potencjalna układu
| (%i1) | TPE=('integrate((1/2)*E*I*'diff(u(x),x,2)^2-w(x)*u(x),x)); |
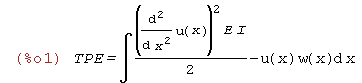
Obciażenie wspornika w(x)=W*x jest liniowe
| (%i2) | w(x):=w$ |
gdzie funkcję u(x) dobramy tak aby spełniała warunki
brzegowe to jest:
dla x=0 u(0)=0
x=0 du/dx=0
oraz
M=EI(d^2u/dx^2)=0 dla x=L
**********************************************
Funkcja aproksymująca "jednoskładnikowa"
**********************************************
| (%i3) | u(x):=C[1]*(x/L)^2; |
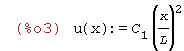
Krok 2
Dla belki wspornikowe siłami pionowymi o intensywności w(x) całkowita energia potencjalna
TPE jest obliczana z:
| (%i4) | TPE:integrate((1/2)*E*I*diff(u(x),x,2)^2-w(x)*u(x),x,0,L); |
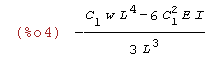
Krok 3
Itotą metody Ritz'a jest obliczanie warotści C1 i C2 dajacych minimum funkcji TPE_
| (%i5) | 'diff(TPE_,C[1])=0; |
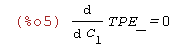
Obliczamy pochode TPE po stałych C1 i C2 i przyrównujemy je do zera
| (%i6) | eq1:diff(TPE,C[1]); |
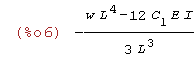
Krok 4
Poszukujemy wartości C1 i C2 po rozwiązaniu układu równań eq1=0 ieq2=0
| (%i7) | roz:solve([eq1=0],[C[1]]); |
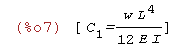
Krok 5
Budujemy ostateczną formę wyrażenia opisujacego linię ugiecia liny u(x)
| (%i8) | C[1]:rhs(roz[1]); |
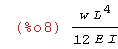
| (%i9) | u(x); |
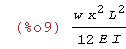
kreślenie lini ugięcia liny
dla L=1 w=1, E=1 I=1
| (%i10) | L:1$ w:1$ E:1;I:1; |

| (%i14) | wxplot2d(-u(x),[x,0,L]); |
Obliczamy wartość momentu gnacego dla końca belki
| (%i15) |
M:E*I*diff(u(x),x,2),numer; M,numer; |

wniosek funkcja u(x) nie spełnia warunku M(L)=0
**********************************************
Funkcja aproksymująca "dwuskładnikowa"
**********************************************
| (%i17) |
kill(all); w(x):=w; |
| (%i2) | u(x):=C[1]*(x/L)^2+C[2]*(x/L)^3; |
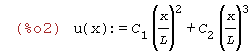
Obliczamy pochodną up(x) funkcji u(x) po x
| (%i3) | upp(x):=diff(u(x),x,2); |
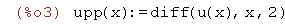
| (%i4) | upp(x); |
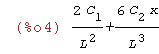
Krok 2
Dla belki wspornikowe siłami pionowymi o intensywności w(x) całkowita energia potencjalna
TPE jest obliczana z:
| (%i5) |
assume(L>0); TPE:integrate((1/2)*E*I*diff(u(x),x,2)^2-w(x)*u(x),x,0,L); |
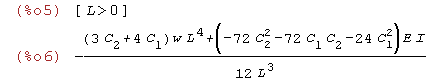
Krok 3
Itotą metody Ritz'a jest obliczanie warotści C1 i C2 dajacych minimum funkcji TPE_
| (%i7) | 'diff(TPE_,C[1])=0; 'diff(TPE_,C[2])=0; |
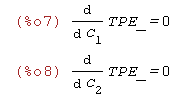
Obliczamy pochode TPE po stałych C1 i C2 i przyrównujemy je do zera
| (%i9) | eq1:diff(TPE,C[1]); eq2:diff(TPE,C[2]); |
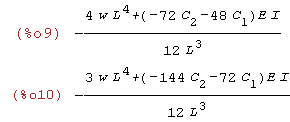
Krok 4
Poszukujemy wartości C1 i C2 po rozwiązaniu układu równań eq1=0 ieq2=0
| (%i11) | roz:solve([eq1=0,eq2=0],[C[1],C[2]]); |
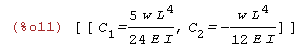
Krok 5
Budujemy ostateczną formę wyrażenia opisujacego linię ugiecia liny u(x)
z uwagi, że otrzymane rozwiązanie składa się z dwu elementów zagnieżdżonych dwukrotnie
stosujemy podwójen indeksowane.
| (%i12) | C[1]:rhs(roz[1][1]); C[2]:rhs(roz[1][2]); |
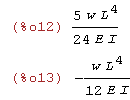
| (%i14) | u(x); |
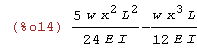
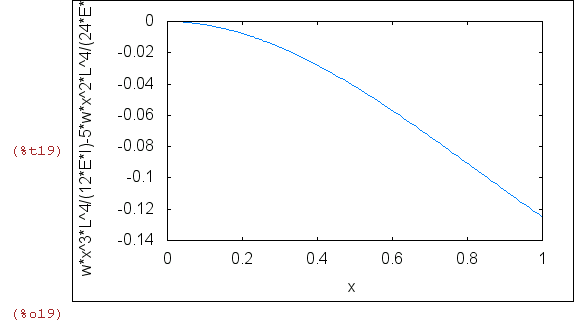
kreślenie lini ugięcia liny
dla L=1 w=1, E=1 I=1
| (%i15) | L:1$ w:1$ E:1$I:1$ |
| (%i19) | wxplot2d(-u(x),[x,0,L]); |
Obliczamy wartość momentu gnacego dla końca belki
| (%i20) |
M:E*I*diff(u(x),x,2),numer; x:L$ M,numer; |
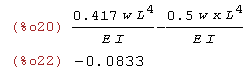
wniosek funkcja u(x) nie spełnia warunku M(L)=0
**********************************************
Funkcja aproksymująca "trójskładnikowa"
**********************************************
| (%i23) |
kill(all)$ w(x):=w$ |
| (%i2) | u(x):=C[1]*(x/L)^2+C[2]*(x/L)^3+C[3]*(x/L)^4; |
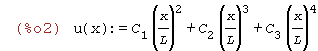
Obliczamy pochodną up(x) funkcji u(x) po x
| (%i3) | upp(x):=diff(u(x),x,2)$ |
| (%i4) | upp(x); |
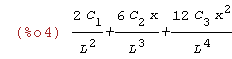
Krok 2
Dla belki wspornikowe siłami pionowymi o intensywności w(x) całkowita energia potencjalna
TPE jest obliczana z:
| (%i5) |
assume(L>0); TPE:integrate((1/2)*E*I*diff(u(x),x,2)^2-w(x)*u(x),x,0,L); |
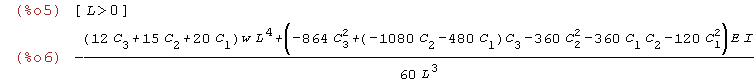
Krok 3
Itotą metody Ritz'a jest obliczanie warotści C1 i C2 dajacych minimum funkcji TPE_
| (%i7) | 'diff(TPE_,C[1])=0; 'diff(TPE_,C[2])=0; 'diff(TPE_,C[3])=0; |

Obliczamy pochode TPE po stałych C1 i C2 i przyrównujemy je do zera
| (%i10) | eq1:diff(TPE,C[1]); eq2:diff(TPE,C[2]); eq3:diff(TPE,C[3]); |
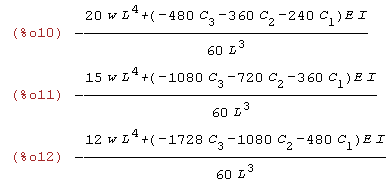
Krok 4
Poszukujemy wartości C1 i C2 po rozwiązaniu układu równań eq1=0 ieq2=0
| (%i13) | roz:solve([eq1=0,eq2=0, eq3=0],[C[1],C[2],C[3]]); |
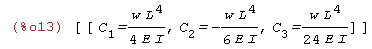
Krok 5
Budujemy ostateczną formę wyrażenia opisujacego linię ugiecia liny u(x)
z uwagi, że otrzymane rozwiązanie składa się z dwu elementów zagnieżdżonych dwukrotnie
stosujemy podwójen indeksowane.
| (%i14) | C[1]:rhs(roz[1][1]); C[2]:rhs(roz[1][2]); C[3]:rhs(roz[1][3]); |
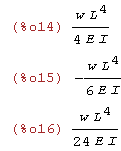
| (%i17) | u(x); |
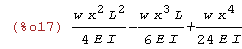
kreślenie lini ugięcia liny
dla L=1 w=1, E=1 I=1
| (%i18) | L:1$ w:1$ E:1$I:1$ |
| (%i22) | wxplot2d(-u(x),[x,0,L]); |
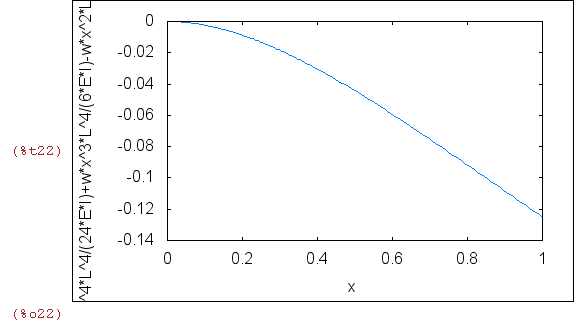
Obliczamy wartość momentu gnacego dla końca belki
| (%i23) |
M:E*I*diff(u(x),x,2),numer; x:L$ M,numer; |
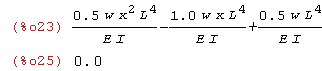
wniosek funkcja u(x) spełnia warunek M(L)=0
rozwiązanie analityczne ma postać u(x) np metodą Clebscha
| (%i26) |
kill(all); u(x):=w*L^2/(24*E*I)*((1-(x/L))^4+4*x/L-1); |
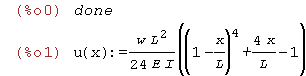
1.4 Zadanie do wykonania (korespondencyjnie)
Zadania do wykonania (korespondencyjnie)
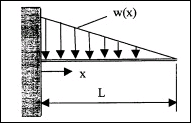
Dla belki wspornikowej o długości L jak nba rysunku i obciążonej obciążeniem ciągłym w(x) (jedn z wariantów)
obliczyc metodą Ritz'a ugięcie porównać do rozwiązania analitycznego ()
przyjąć wielomian aproksymacyjny przynajmniej dwuskładnikowy
Figure 3: E:\praca\Maxima_w_przykladach\MetodaRitza_Galerkina\Ritz\Ritz_wspornik_1.jpg
| (%i2) | w(x):=w[0]*(1-x/L); |
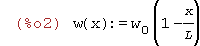
| (%i3) | w(x):=w[0]*(1-x/L)^2; |
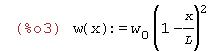
| (%i4) | w(x):=w[0]*(1-x/L)^3; |
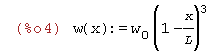
| (%i5) | w(x):=w[0]*sin(x/L); |
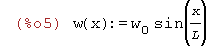
| (%i6) | w(x):=w[0]*(x/L)^2; |
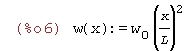
| (%i7) | w(x):=w[0]*(x/L)^3; |